Womit wir uns beschäftigen
Abgeschlossene Projekte
Projekt MALU
Im Projekt MALU (Mathe AG an der Leibniz Universität Hannover) wurden seit dem WS 2008/09 mathematisch interessierte und verschieden begabte Fünftklässler im Problemlösen gefördert. Wir führten dazu in allen fünften Klassen an vier Hannoveraner Gymnasien je einen allgemeinen und einen mathematischen Begabungstest durch und luden daraufhin verschieden mathematisch begabte Kinder zur Teilnahme an der AG ein. Die Problembearbeitungsprozesse der Fünftklässler-Paare wurden aufgezeichnet und im Rahmen der Begleitforschung zum MALU-Projekt daraufhin untersucht, welche Zusammenhänge z.B. von Kooperationsverhalten und Heurismengebrauch mit dem Problemlöseerfolg bestehen.






Das Projekt HeuRekAP
Im Hannoveraner Projekt HeuRekAP (Heuristische Rekonstruktion von Aufgaben zum Problemlösen) wurden Aufgaben für ein Heuristik-Training aufbereitet und unterrichtlich erprobt (D. Brockmann-Behnsen und Prof. Dr. T. Gawlick in Kooperation mit H.-J. Elschenbroich).
Mehr Informationen zum Projekt finden Sie hier.






Aktuelle Projekte
Das Projekt LeduPro
Das Projekt LeduPro (Lernen durch Problemlösen) dient der Schaffung von Lerngelegenheiten für das Problemlösen. Denn das Problemlösen ist ja eine im Hinblick auf den allgemeinbildenden Charakter des Mathematikunterrichts wichtige und fächerübergreifende Kompetenz, die im Mathematikunterricht erworben werden soll - allerdings mangelt es nach Rückmeldung aus der Schulpraxis hierzu oftmals an Lerngelegenheiten, was insbesondere zu einer fehlenden Vernetzung mathematischen Wissens führt.
Hier finden Sie die vollständige Projektbeschreibung.






Projekt Begabtenförderung und Leibniz-Kurs Mathematik
Leibniz-Kurs Mathematik
Das Projekt MALU ging im Sommer 2013 in so genannte Knobelkurse: Das sind Arbeitsgemeinschaften an Schulen im Raum Hannover, die sich über jeweils ein Schuljahr erstrecken und von Lehramtsstudierenden geleitet werden, die von uns ausgewählt und unterstützt werden. Die Knobelkurse sind ein Angebot des Vereins Forschergeist e.V. Dort kann man sich auch für einen Kurs anmelden.
Der Leibniz-Kurs Mathematik ist ein gemeinsames Angebot mit dem Verein Forschergeist. Er findet an der Leibniz-Universität statt. Im Anschluss an das Projekt LeduPro werden hier gezielt heuristische Strategien vermittelt und gemeinsam Wettbewerbsaufgaben gelöst. Teilnehmende des Leibniz-Kurses haben auch bereits erfolgreich am Bolyai-Wettbewerb teilgenommen.






Hinweis: Wir suchen immer wieder Lehramtsstudierende, die Zeit und Interesse haben, einen Knobelkurs zu betreuen. Da Forschergeist die Betreuung auf Honorarbasis vergütet, kann die Tätigkeit problemlos neben einer bestehenden Hilfskraft- oder schulischen Anstellung ausgeübt werden, ohne dass dafür die Freibeträge überschritten werden.
Bei Rückfragen wenden Sie sich bitte an Frau Hilgers (E-Mail: hilgers@idmp.uni-hannover.de).
Sichtweisen auf die Aufgabe P1
Die Aufgabe P1 hat viele interessante Lösungswege. Nehmen Sie sich doch Zettel und Stift und probieren Sie sich selbst an der Aufgabe aus. Sollten Sie es nicht schaffen oder gespannt sein, welche Möglichkeiten es noch gibt, können Sie hier mit Hilfe einer Animation einen der möglichen Lösungswege erkunden. Zu der Animation stehen rechts einige Fragen, die Ihnen dabei helfen können. Zudem können Sie sich ein Poster ansehen, welches tiefere Einblicke bietet.
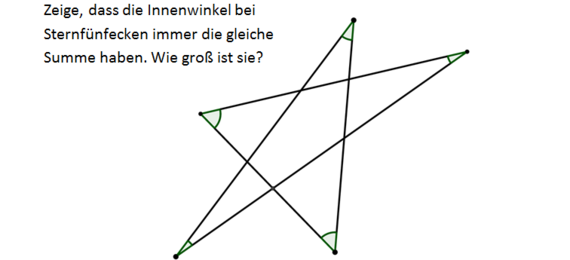

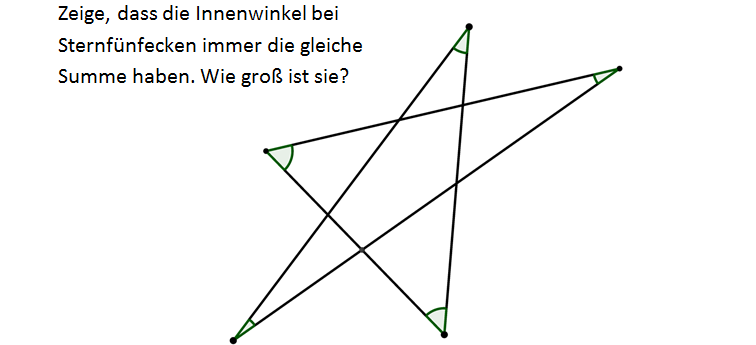
Beobachten Sie die Animation!
-
Was verändert sich? Was bleibt gleich?
Mir fällt auf, dass sich die Streckenlängen im Dreieck, das sich bewegt, ändern. Aber die interessieren mich nicht, ich möchte ja irgendwas mit Winkeln erreichen. Also wie ändern sich die Winkel? Die Markierung soll mir wahrscheinlich weismachen, dass sich der grüne Winkel nicht ändert. Und für die zwei Stellen, bei denen das Dreieck in der Ebene des Sternfünfecks liegt, muss das ja, wegen des Scheitelwinkelsatzes, auch stimmen. Doch was ist mit den anderen beiden Winkeln?
-
Welche Teile der Animation können Sie nutzen? Können Sie die Aufgabe in einem Spezialfall lösen?
Fest steht ja schon mal, dass ich nur die Stellen nutzen kann, bei denen das Dreieck in der Ebene des Sternfünfecks liegt. In allen anderen Fällen ist es ja kein Sternfünfeck mehr. Das heißt, ich habe zwei Dreiecke. Was passiert nun, wenn die Winkel in dem Dreieck, das sich bewegt, gleich bleiben? Dann transportiere ich die Winkel ja von einem in ein anderes Dreieck. Was hilft mir dieses andere Dreieck denn mehr? Wenn ich davon ausgehe, dass beim Transport alle Winkel gleich bleiben, dann finde ich ein Dreieck, dessen Winkelsumme gleich der Summe der Innenwinkel des Sternfünfecks ist (Versuchen Sie herauszufinden, welches Dreieck ich hier meine!). Und da die Innenwinkelsumme eines Dreiecks 180° ist, heißt das, dass auch die Innenwinkelsumme des Sternenfünfecks 180° sein muss!
-
Was muss nun gelten, damit die Aussage auch im allgemeinen Fall gilt?
Ich kann die Winkel im ersten Dreieck CEF ja ändern, ohne dass sich die Winkel im anderen Dreieck ABF ändern (Überzeugen Sie sich davon!). Nur der grüne Winkel ändert sich bestimmt nicht, das habe ich eben schon herausgefunden. Was muss jetzt gelten, damit die Innenwinkelsumme des Sternfünfecks auch dann 180° ist, wenn sich die Winkel beim Transport verändern? Dann muss ja die Summe der beiden Winkel, die nicht grün sind, in dem Dreieck, das sich bewegt, gleich bleiben! Aber das muss ja stimmen, da die Innenwinkelsumme im Dreieck 180° ist und der grüne Winkel gleich bleibt! Also ist die Innenwinkelsumme im Sternfünfeck – unabhängig davon, ob die Winkel beim Transport gleich bleiben oder nicht – 180°.
Dies ist die Aufgabe, die an der Tafel steht. Es gibt nicht nur geschickte Rechenwege, sondern auch interessante zahlentheoretische Bezüge.






